皆さま、こんにちは！
ワクワク経営ナビゲーターの古屋早雪です。

今日もパーティーが宿屋で話をしています。
旅芸人「というわけで、1日で最も稼げる方法を考えたいと思うんだ」
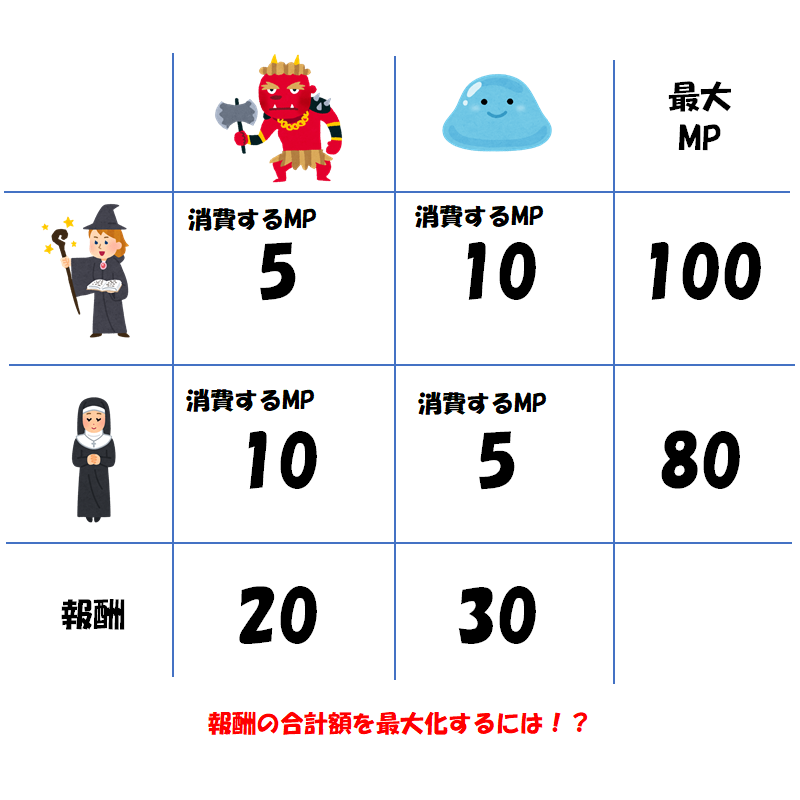
魔法使い「退治の依頼が出ている魔物はゴブリンとスライムね。ゴブリンは1体20G、スライムは1体30Gの報酬がもらえるわ」
武闘家「じゃあ、できるだけスライムを倒した方がいいんじゃねぇか？」
戦士「スライムは物理攻撃が効きにくいから、魔法使い頼みになるな」
魔法使い「スライムだと、1体でMPを10は使うわね」
戦士「ゴブリンだとどうだ？」
魔法使い「ゴブリンなら物理攻撃で削れるから、あたしのMPは5で済むわ」
武闘家「ってことは、ゴブリンを多く倒した方がいいんじゃねぇか？」
旅芸人「いや、そうとも限らないかな。ゴブリンの方が攻撃が強いから、回復に使うMP消費が大きいんだ」
僧侶「そうですね。。。スライムなら1体でMP5で済みますが、ゴブリンはMP10必要です」
武闘家「ってことは、どっちを多く倒した方がいいんだ？」
旅芸人「こういうときは、グラフを描くといいんだ」

さて、2つ以上の制約がある場合に、成果を最大にする組み合わせを算出する時、線形計画法という方法を使うことが有効です。
例えば、工場などで2種類の加工が必要な2つの製品があり、各製品の各加工にかかる時間が異なる、各加工をおこなえる時間が限られているという場合、利益を最大化するための製品ごとの生産量の組み合わせを算出する際、線形計画法を使うことがあります。
前述のお話でいうと、2つの製品が「スライム」と「ゴブリン」に対応し、2種類の加工が「魔法使いのMP消費」と「僧侶のMP消費」に対応します。

ここで、ゴブリンをX体、スライムをY体退治したとします。
この時、魔法使いのMP消費は
5X＋10Y
となりますので、魔法使いの最大MPが100だとすると、
5X＋10Y＜100
の制約が発生します。
同様に、僧侶のMP消費は
10X＋5Y
なので、僧侶の最大MPが80だとすると
10X＋5Y＜80
の制約があります。

この範囲の中で、報酬を最大化するには、合計報酬額をあらわす
20X+30Y
が最大となる点を取ればよいことになりますが、これは結論としては、先ほどの不等式の境界線、つまり不等号を等号に置き換えた2つの直線の交点となります。

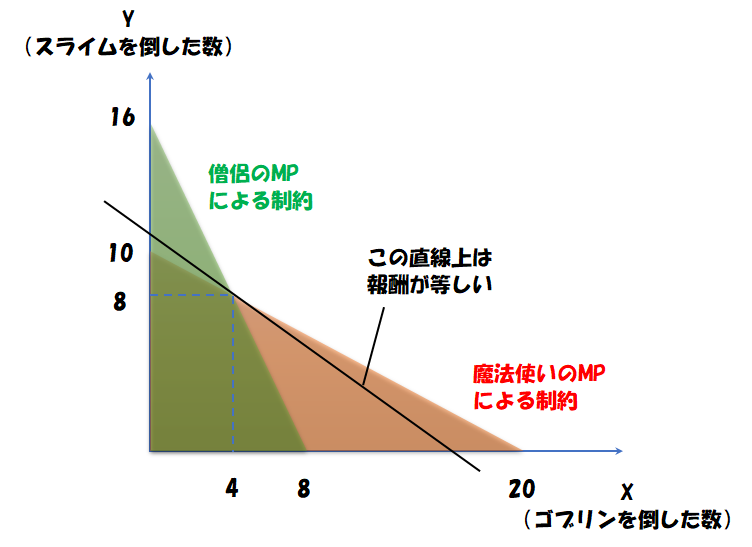
このように、複数の制約がある中で最適の組み合わせを見つけるために、様々な場面で線形計画法を使うことができます。
また、グラフで表すと直感的に理解することができますね！

是非、線形計画法をうまく使って、ワクワクを最大化する方法を考えてみてくださいね♪